MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS [940]

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS.

MECÃNICA GRACELI GERAL - QTDRC.

$equação Graceli dimensional relativista tensorial quântica de campos$

$\psi ^{*}$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

/ $\psi ^{*}$ [ $\psi ^{*}$

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS. EM ;

Comportamento da força forte[editar | editar código-fonte]

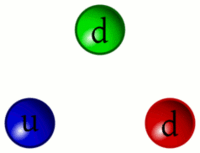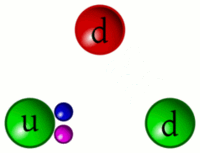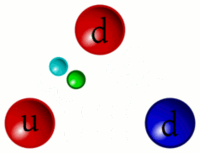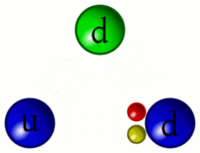
A interação de quarks de um nêutron deve-se à força forte./ *$\psi ^{*}$* [ *$\psi ^{*}$*

{\displaystyle \psi ^{*}} — A interação de quarks de um nêutron deve-se à força forte./ *$\psi ^{*}$* [ *$\psi ^{*}$*

A forte força contemporânea é descrita pela cromodinâmica quântica (sigla QCD, em inglês), sendo parte do modelo padrão da física de partículas. Matematicamente, a QCD é uma teoria de calibre não abeliana, com base em um calibre (local) de grupo de simetria chamado SU (3).

Os quarks e glúons são as únicas partículas que não têm o desaparecimento da carga e cor, podendo então participarem da forte interação, sendo que esta atua diretamente nestes.

A força forte, ao contrário das outras forças fundamentais da natureza (eletromagnética, fraca e gravidade) não fica menos poderosa com a distância de seu alcance (que é do tamanho de um hádron), a sua força de atuação é de cerca de 10000 N, em QCD isto é chamado confinamento da cor, mas implica que somente hádrons e não quarks individuais podem ser observados. A explicação é que a quantidade de trabalho realizado contra uma força de 10 000 newtons (sobre o peso de uma tonelada métrica de massa sobre a superfície da Terra) é o suficiente para criar novas partículas pelo choque entre elas. Em termos simples a própria energia aplicada para puxar dois quarks separados irá gerar um novo par de quarks. O fracasso em observar quarks livres é uma evidência desse fenômeno.

A dinâmica dos quarks e glúons é controlada pela lagrangiana da cromodinâmica quântica. A lagrangiana invariante de gauge da QCD é

${\mathcal {L}}_{\mathrm {QCD} }={\bar {\psi }}_{i}\left(i(\gamma ^{\mu }D_{\mu })_{ij}-m\,\delta _{ij}\right)\psi _{j}-{\frac {1}{4}}G_{\mu \nu }^{a}G_{a}^{\mu \nu }$

onde $\psi _{i}(x)\,$ são os campos dos quarkos, uma função dinâmica do espaço tempo, na representação fundamental dogrupo de gauge SU(3), indexada por $i,\,j,\,\ldots$ ; ${\mathcal {A}}_{\mu }^{a}(x)\,$ são os campos de glúons, também funções dinâmicas do espaço-tempo, na representação adjunta do grupo de gauge SU(3), indexado por a, b,... ; γ^μ são as matrizes de Dirac conectando a representação spinorial a representação vetorial do grupo de Lorentz.

O símbolo $G_{\mu \nu }^{a}\,$ representa o tensor de força do campo de glúon invariante de gauge, análogo ao tensor de força do campo eletromagnético, F^{\mu \nu} \,, em eletrodinâmica quântica. É dado por:^[8]

Matematicamente, o eletromagnetismo é unificado com as interações fracas como um campo de Yang-Mills com um grupo de calibre SU(2) × U(1) , que descreve as operações formais que podem ser aplicadas aos campos de calibre eletrofracos sem alterar a dinâmica do sistema. Estes domínios são os campos de isospin fraco W₁, W₂, e W₃, e o campo de hipercarga fraca B. Essa invariância é conhecida como simetria eletrofraca.

Os geradores de SU(2) e U(1) recebem o nome de isospin fraco (chamado de T) e hipercarga fraca (chamada de Y), respectivamente. Estes então dão origem aos bósons de calibre que medeiam as interações eletrofracas - os três bósons W de isospin fraco W₁, W₂, e W₃ e o bóson B de hipercarga fraca, respectivamente, todos os quais são "inicialmente" sem massa. Esses ainda não são campos físicos, antes da quebra espontânea da simetria e do mecanismo de Higgs associado.

No modelo padrão, os bósons W^± e Z⁰ e o fóton são produzidos por meio da quebra espontânea de simetria eletrofraca SU(2) × U(1)_Y a U(1)_em, efetuada pelo mecanismo de Higgs (ver também bóson de Higgs), um elaborado fenômeno teórico de campo quântico que "espontaneamente" altera a realização da simetria e reorganiza os graus de liberdade.^[6]^[7]^[8]^[9]

A carga elétrica surge como uma combinação linear (não trivial) de Y (hipercarga fraca) e o componente T₃ do isospin fraco ( $Q=T_{3}+{\tfrac {1}{2}}Y_{\mathrm {W} }$ ) que não se acopla ao bóson de Higgs - ou seja, o Higgs e o campo eletromagnético não têm efeito um sobre o outro no nível das forças fundamentais ("nível de árvore"), enquanto qualquer outra combinação linear da hipercarga e do isospin fraco irá interagir com o Higgs. Isso causa uma separação aparente entre a força fraca, que interage com o Higgs, e o eletromagnetismo, que não interage. Matematicamente, a carga elétrica é uma combinação específica da hipercarga e T₃ delineada na figura.

U(1)_em (o grupo de simetria do eletromagnetismo) é definido como o grupo gerado por esta combinação linear especial, e a simetria descrita por este grupo é ininterrupta, uma vez que não interage diretamente com o Higgs (mas o faz por meio de flutuações quânticas).

A quebra espontânea de simetria acima faz com que os bósons W₃ e B se aglutinem em dois bósons físicos diferentes com massas diferentes - o bóson Z₀ e o fóton (γ),

{\begin{pmatrix}\gamma \\Z^{0}\end{pmatrix}}={\begin{pmatrix}\cos \theta _{\text{W}}&\sin \theta _{\text{W}}\\-\sin \theta _{\text{W}}&\cos \theta _{\text{W}}\end{pmatrix}}{\begin{pmatrix}B\\W_{3}\end{pmatrix}},

/ $\psi ^{*}$ [ $\psi ^{*}$

onde $θ W$ é o ângulo de mistura eletrofraca. Os eixos que representam as partículas, essencialmente apenas foram rodados no plano (W₃, B) pelo ângulo $θ W$ . Isso também introduz uma incompatibilidade entre as massas das partículas
Z0
e
W±
(denotadas como $M Z$ e $M W$ , respectivamente),

M_{\text{Z}}={\frac {M_{\text{W}}}{\cos \theta _{\text{W}}}}.

/ $\psi ^{*}$ [ $\psi ^{*}$

Os bósons $W 1$ e $W 2$ , por sua vez, combinam-se para produzir bósons massivos carregados

W^{\pm }={\frac {1}{\sqrt {2}}}(W_{1}\mp iW_{2}).

/ $\psi ^{*}$ [ $\psi ^{*}$

Lagrangiano[editar | editar código-fonte]

Antes da quebra de simetria eletrofraca[editar | editar código-fonte]

O Lagrangiano para as interações eletrofracas é dividido em quatro partes antes que a quebra de simetria eletrofraca se manifeste,

{\mathcal {L}}_{\text{EW}}={\mathcal {L}}_{g}+{\mathcal {L}}_{f}+{\mathcal {L}}_{h}+{\mathcal {L}}_{y}~.

/ $\psi ^{*}$ [ $\psi ^{*}$

O termo ${\mathcal {L}}_{g}$ descreve a interação entre os três bósons vetoriais W e o bóson vetorial B,

{\mathcal {L}}_{g}=-{\tfrac {1}{4}}W_{a}^{\mu \nu }W_{\mu \nu }^{a}-{\tfrac {1}{4}}B^{\mu \nu }B_{\mu \nu }

/ $\psi ^{*}$ [ $\psi ^{*}$

onde $W^{a\mu \nu }$ ( $a=1,2,3$ ) e $B^{\mu \nu }$ são os tensores de intensidade de campo para os campos de calibre de isospin fraco e hipercarga fraca.

${\mathcal {L}}_{f}$ é o termo cinético para o Modelo Padrão de férmions. A interação entre os bósons de calibre e os férmions se dão pela derivade covariante de calibre,

{\mathcal {L}}_{f}={\overline {Q}}_{i}iD\!\!\!\!/\;Q_{i}+{\overline {u}}_{i}iD\!\!\!\!/\;u_{i}+{\overline {d}}_{i}iD\!\!\!\!/\;d_{i}+{\overline {L}}_{i}iD\!\!\!\!/\;L_{i}+{\overline {e}}_{i}iD\!\!\!\!/\;e_{i}

/ $\psi ^{*}$ [ $\psi ^{*}$

onde o subscrito i percorre as três gerações de férmions; Q, u e d são os campos de quarks correspondendo ao dubleto levógiro, singleto dextrógiro up, e singleto dextrógiro down; e L e e são os campos de elétrons do dubleto levógiro e singleto dextrógiro. A barra de Feynman $D\!\!\!\!/$ significa a contração do quadri-gradiente com as matrizes de Dirac

D\!\!\!\!/=\gamma ^{\mu }D_{\mu }

/ $\psi ^{*}$ [ $\psi ^{*}$

e a derivada covariante é (excluindo o campo de calibre do glúon para a interação forte)

D_{\mu }:=\partial _{\mu }-i{\frac {g'}{2}}Y\,B_{\mu }-i{\frac {g}{2}}T_{j}\,W_{\mu }^{j}

/ $\psi ^{*}$ [ $\psi ^{*}$

Aqui $�$ é a hipercarga fracais e $T_{j}$ são os componentes do isospin fraco.

O termo ${\mathcal {L}}_{h}$ descreve o campo de Higgs e suas interações consigo mesmo e com os bósons de calibre,

{\mathcal {L}}_{h}=|D_{\mu }h|^{2}-\lambda \left(|h|^{2}-{\frac {v^{2}}{2}}\right)^{2}

/ $\psi ^{*}$ [ $\psi ^{*}$

O termo ${\mathcal {L}}_{y}$ descreve a interação de Yukawa com os férmions,

{\mathcal {L}}_{y}=-y_{u\,ij}\epsilon ^{ab}\,h_{b}^{\dagger }\,{\overline {Q}}_{ia}u_{j}^{c}-y_{d\,ij}\,h\,{\overline {Q}}_{i}d_{j}^{c}-y_{e\,ij}\,h\,{\overline {L}}_{i}e_{j}^{c}+h.c.~,

/ $\psi ^{*}$ [ $\psi ^{*}$

e gera suas massas, manifestas quando o campo de Higgs adquire um valor esperado do vácuo diferente de zero, discutido a seguir.

Depois da quebra de simetria eletrofraca[editar | editar código-fonte]

O Lagrangiano se reorganiza à medida que o bóson de Higgs adquire um valor esperado do vácuo diferente do zero, ditado pelo potencial da seção anterior. Como resultado dessa reescrita, a quebra de simetria se torna manifesta. Na história do universo, acredita-se que isso tenha acontecido logo após o big bang quente, quando o universo estava a uma temperatura de 159,5±1,5 GeV^[10] (assumindo o Modelo Padrão da física de partículas).

Devido à sua complexidade, este Lagrangiano é melhor descrito dividindo-o em várias partes como segue.

{\mathcal {L}}_{\text{EW}}={\mathcal {L}}_{\text{K}}+{\mathcal {L}}_{\text{N}}+{\mathcal {L}}_{\text{C}}+{\mathcal {L}}_{\text{H}}+{\mathcal {L}}_{\text{HV}}+{\mathcal {L}}_{\text{WWV}}+{\mathcal {L}}_{\text{WWVV}}+{\mathcal {L}}_{\text{Y}}.

/ $\psi ^{*}$ [ $\psi ^{*}$

O termo cinético ${\mathcal {L}}_{K}$ contém todos os termos quadráticos da Lagrangiana, que incluem os termos dinâmicos (as derivadas parciais) e os termos de massa (visivelmente ausentes da Lagrangiana antes da quebra de simetria)

{\begin{aligned}{\mathcal {L}}_{\text{K}}=\sum _{f}{\overline {f}}(i\partial \!\!\!/\!\;-m_{f})f-{\frac {1}{4}}A_{\mu \nu }A^{\mu \nu }-{\frac {1}{2}}W_{\mu \nu }^{+}W^{-\mu \nu }+m_{W}^{2}W_{\mu }^{+}W^{-\mu }\\\qquad -{\frac {1}{4}}Z_{\mu \nu }Z^{\mu \nu }+{\frac {1}{2}}m_{Z}^{2}Z_{\mu }Z^{\mu }+{\frac {1}{2}}(\partial ^{\mu }H)(\partial _{\mu }H)-{\frac {1}{2}}m_{H}^{2}H^{2}~,\end{aligned}}

/ $\psi ^{*}$ [ $\psi ^{*}$

onde a soma percorre todos os férmions da teoria (quarks e léptons), e os campos $A_{\mu \nu }$ , $Z_{\mu \nu }$ , $W_{\mu \nu }^{-}$ , and $W_{\mu \nu }^{+}\equiv (W_{\mu \nu }^{-})^{\dagger }$ são dados como

X_{\mu \nu }^{a}=\partial _{\mu }X_{\nu }^{a}-\partial _{\nu }X_{\mu }^{a}+gf^{abc}X_{\mu }^{b}X_{\nu }^{c}~,

/ $\psi ^{*}$ [ $\psi ^{*}$

com ‘ $�$ ’ a ser substituído pelo campo relevante ( $�$ , $�$ , $W^{\pm }$ ), e $f abc$ pelas constantes de estrutura do grupo de calibres apropriado.

As componentes do Lagrangiano para a corrente neutra ${\mathcal {L}}_{\text{N}}$ e para a corrente carregada ${\mathcal {L}}_{\text{C}}$ contêm as interações entre os férmions e os bósons de calibre,

{\mathcal {L}}_{\text{N}}=eJ_{\mu }^{\text{em}}A^{\mu }+{\frac {g}{\cos \theta _{W}}}(J_{\mu }^{3}-\sin ^{2}\theta _{W}J_{\mu }^{\text{em}})Z^{\mu }\,,

/ $\psi ^{*}$ [ $\psi ^{*}$

onde $e=g\sin \theta _{\text{W}}=g'\cos \theta _{\text{W}}\,.$ A corrente eletromagnética $J_{\mu }^{\text{em}}$ é

J_{\mu }^{\text{em}}=\sum _{f}q_{f}{\overline {f}}\gamma _{\mu }f

/ $\psi ^{*}$ [ $\psi ^{*}$

onde $q_{f}^{}$ são as cargas elétricas dos férmions. A corrente neutra fraca $J_{\mu }^{3}$ é

J_{\mu }^{3}=\sum _{f}I_{f}^{3}{\overline {f}}\gamma _{\mu }{\frac {1-\gamma ^{5}}{2}}f

/ $\psi ^{*}$ [ $\psi ^{*}$

onde $I_{f}^{3}$ é o isospin fraco dos férmions.

A parte da corrente carregada da Lagrangiana é dada por

{\mathcal {L}}_{\text{C}}=-{\frac {g}{\sqrt {2}}}\left[{\overline {u}}_{i}\gamma ^{\mu }{\frac {1-\gamma ^{5}}{2}}M_{ij}^{\text{CKM}}d_{j}+{\overline {\nu }}_{i}\gamma ^{\mu }{\frac {1-\gamma ^{5}}{2}}e_{i}\right]W_{\mu }^{+}+{\text{h.c.}}~,

/ $\psi ^{*}$ [ $\psi ^{*}$

onde ${\mathcal {L}}_{\text{H}}$ contém os termos de auto interação de três e quatro pontos de Higgs,

{\mathcal {L}}_{\text{H}}=-{\frac {gm_{H}^{2}}{4m_{W}}}H^{3}-{\frac {g^{2}m_{H}^{2}}{32m_{W}^{2}}}H^{4}~.

/ $\psi ^{*}$ [ $\psi ^{*}$

${\mathcal {L}}_{\text{HV}}$ contém as interações de Higgs com os bósons vetoriais de calibre,

{\mathcal {L}}_{\text{HV}}=\left(gm_{W}H+{\frac {g^{2}}{4}}H^{2}\right)\left(W_{\mu }^{+}W^{-\mu }+{\frac {1}{2\cos ^{2}\theta _{W}}}Z_{\mu }Z^{\mu }\right).

/ $\psi ^{*}$ [ $\psi ^{*}$

${\mathcal {L}}_{\text{WWV}}$ contém as auto interações de três pontos de calibre,

{\mathcal {L}}_{\text{WWV}}=-ig[(W_{\mu \nu }^{+}W^{-\mu }-W^{+\mu }W_{\mu \nu }^{-})(A^{\nu }\sin \theta _{W}-Z^{\nu }\cos \theta _{W})+W_{\nu }^{-}W_{\mu }^{+}(A^{\mu \nu }\sin \theta _{W}-Z^{\mu \nu }\cos \theta _{W})].

${\mathcal {L}}_{\text{WWVV}}$ contém as auto interações de quatro pontos de calibre,

{\begin{aligned}{\mathcal {L}}_{\text{WWVV}}=-{\frac {g^{2}}{4}}{\Big \{}&[2W_{\mu }^{+}W^{-\mu }+(A_{\mu }\sin \theta _{W}-Z_{\mu }\cos \theta _{W})^{2}]^{2}\\&-[W_{\mu }^{+}W_{\nu }^{-}+W_{\nu }^{+}W_{\mu }^{-}+(A_{\mu }\sin \theta _{W}-Z_{\mu }\cos \theta _{W})(A_{\nu }\sin \theta _{W}-Z_{\nu }\cos \theta _{W})]^{2}{\Big \}}.\end{aligned}}

${\mathcal {L}}_{\text{Y}}$ contém as interações Yukawa entre os férmions e o campo de Higgs,

{\mathcal {L}}_{\text{Y}}=-\sum _{f}{\frac {gm_{f}}{2m_{W}}}{\overline {f}}fH.

/ $\psi ^{*}$ [ $\psi ^{*}$

Note os fatores ${\tfrac {1}{2}}(1-\gamma ^{5})$ nos acoplamentos fracos: esses fatores projetam os componentes levógiros dos campos de spinor. É por isso que se diz que a teoria eletrofraca é uma teoria quiral.

Max Planck obteve a forma correta da distribuição porque postulou a quantização da energia dos osciladores harmônicos que comporiam as paredes da cavidade que confina a radiação. Essa hipótese teve por efeito introduzir um limite máximo de freqüência acima do qual há um corte (cutoff) nas contribuições dos entes (ondas eletromagnéticas) que estão em equilíbrio.

Einstein, para explicar o efeito fotoelétrico, ampliou o conceito da quantização para a energia radiante, postulando a existência do fóton (o que "implicitamente" quer dizer que as equações de Maxwell não tem validade ilimitada, porque a existência do fóton implica não-linearidades).

A antiga teoria quântica cedeu lugar à mecânica quântica moderna quando Schrödinger desenvolveu a famosa equação que leva o seu nome. Entretanto, a primeira versão que ele desenvolveu foi a equação que hoje é conhecida como equação de Klein-Gordon, que é uma equação relativista, mas que não descrevia bem o átomo de hidrogênio, por razões que só mais tarde puderam ser entendidas. Assim, ele abandonou a primeira tentativa, chegando à sua equação (equação de Schrödinger):

\left[-{\frac {\hbar ^{2}\nabla ^{2}}{2m}}+V\left(\mathbf {r} ,t\right)\right]\Psi \left(\mathbf {r} ,t\right)=i\hbar {\frac {\partial \Psi \left(\mathbf {r} ,t\right)}{\partial t}}

A equação de Schrödinger acima colocada é a equação "dependente do tempo", pois o tempo aparece explicitamente. Neste caso, as soluções $\Psi$ são funções das coordenadas espaciais e do tempo.

Quando o potencial $\mathbf {V}$ não depende do tempo, ou seja, quando o campo de força ao qual a partícula está submetida é conservativo, é possível separar as variáveis $\mathbf {r}$ e $\mathbf {t}$ .

A equação que a parte espacial da função de onda $\Psi$ obedece é:

\left[-{\frac {\hbar ^{2}\nabla ^{2}}{2m}}+V\left(\mathbf {r} \right)\right]\psi \left(\mathbf {r} \right)=E\psi \left(\mathbf {r} \right)

conhecida como equação de Schrödinger "independente do tempo". Esta é uma equação de autovalores, ou seja, através dela se obtêm simultaneamente autofunções (no caso as funções de onda $\psi$ ) e autovalores (no caso, o conjunto das energias estacionárias $�$ ).

Formulação matemática[editar | editar código-fonte]

Mecânica clássica e mecânica quântica[editar | editar código-fonte]

A dinâmica de uma partícula pontual de massa $�$ em um regime não-relativístico, ou seja, em velocidades muito menores que a velocidade da luz, pode ser determinada através da função lagrangiana^[6]^[7]

$L={\frac {1}{2}}m({\dot {q}}^{i})^{2}-V(q)$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

em que $(q^{i},{\dot {q}}^{i})$ (que são respectivamente coordenadas generalizadas para a posição e a velocidade da partícula) determinam o espaço de fase do sistema e $V(q)$ é o potencial em que a partícula se move. Minimizando o funcional ação

$S=\int dtL(q,{\dot {q}})$

encontra-se a equação de movimento para esse sistema,

$m{\frac {d^{2}q^{i}}{dt^{2}}}=-{\frac {\partial V(q)}{\partial q^{i}}}$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

que é a equação de Newton, desde que $\mathbf {F} =-\nabla V(q)$ .

Existe outra formulação equivalente da mecânica clássica, conhecida como formulação hamiltoniana e que pode ser diretamente relacionada a formulação lagrangiana acima. Para se fazer contato entre as duas formulações, define-se o momento

$p^{i}={\frac {\partial L}{\partial {\dot {q}}^{i}}}$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

de maneira que a função hamiltoniana é dada por

$H(q,p)=p^{i}{\dot {q}}^{i}-L(q^{i},{\dot {q}}^{i})$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

que para a escolha da lagrangiana acima, tem-se

$H(q,p)={\frac {(p^{i})^{2}}{2m}}+V(q)$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Assim como no caso da função lagrangiana, a hamiltoniana descreve toda a dinâmica de um sistema clássico, portanto, considerando uma variação de $H(q^{i},p^{i})$ tem-se um par de equações diferenciais de primeira ordem conhecidas como equações de Hamilton

${\dot {q}}^{i}={\frac {\partial H}{\partial p^{i}}},\quad {\dot {p}}^{i}=-{\frac {\partial H}{\partial q^{i}}}$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

e que equivale a equação de Newton, que é de segunda ordem. No formalismo hamiltoniano, usando a regra da cadeia, pode-se escrever qualquer variação temporal de uma função $F=F(t;q(t);{\dot {q}}(t))$ , em termos das equações de Hamilton acima, de modo que,

${\begin{aligned}{\dot {F}}&={\frac {\partial F}{\partial t}}+{\frac {\partial F}{\partial q^{i}}}{\dot {q^{i}}}+{\frac {\partial F}{\partial p^{i}}}{\dot {p^{i}}}\\&={\frac {\partial F}{\partial t}}+{\frac {\partial F}{\partial q^{i}}}{\frac {\partial H}{\partial p^{i}}}-{\frac {\partial F}{\partial p^{i}}}{\frac {\partial H}{\partial q^{i}}}\\&={\frac {\partial F}{\partial t}}+\{H,F\},\end{aligned}}$

$\psi ^{*}$

onde o parêntese de Poisson é definido como

$\{A,B\}={\frac {\partial A}{\partial p^{i}}}{\frac {\partial B}{\partial q^{i}}}-{\frac {\partial A}{\partial q^{i}}}{\frac {\partial B}{\partial p^{i}}}$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Existem diversas maneiras de realizar a quantização de um sistema clássico, tais como quantização por integrais funcionais e quantização canônica. Esse último método em particular, consiste na substituição do parêntese de Poisson por comutadores^[8]

$\{A,B\}\to {\frac {i}{\hbar }}[{\hat {A}},{\hat {B}}]$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

onde ${\hat {A}},{\hat {B}}$ , são operadores num espaço de Hilbert. Com essas substituições, o parêntese de Poisson entre duas coordenadas generalizadas torna-se

$[{\hat {p}}^{i},{\hat {q}}^{j}]=-i\hbar \delta ^{ij}$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Um aspecto importante a ser observado é que os operadores ${\hat {p}}^{i}$ e ${\hat {E}}$ podem ser representados como os operadores diferencias

${\hat {p}}^{i}=-i\hbar {\frac {\partial }{\partial q^{i}}},\quad ,{\hat {E}}=i\hbar {\frac {\partial }{\partial t}}$

de maneira que a função hamiltoniana, torna-se um operador no espaço de Hilbert, chamado operador hamiltoniano que atua em uma função $\psi (q,t)$

$\left(-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+{\hat {V}}(q)\right)\psi =i\hbar {\frac {\partial \psi }{\partial t}}$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

que é a equação de Schrödinger.

Teoria Clássica de Campos[editar | editar código-fonte]

A formulação lagrangiana e a hamiltoniana da mecânica clássica são refinamentos da mecânica newtoniana e permite o tratamento de sistemas com um número finito de graus de liberdade. Considerando um sistema mecânico unidimensional com $�$ graus de liberdade, que consiste de $�$ partículas pontuais de massa $�$ , separadas por uma distância $\epsilon$ e conectadas entre si por uma mola de constante elástica $\kappa$ . A lagrangiana para esse sistema é:

$L=\sum _{i=1}^{N}\left[{\frac {1}{2}}m{\dot {x}}^{2}-{\frac {\kappa }{2}}(x_{i}-x_{i+1})^{2}\right]$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Esse sistema pode ser estendido facilmente para o limite em que $N\to \infty$ e $L=\epsilon N\to \infty$ . No entanto, se o comprimento total do sistema estiver fixo, tem-se o limite contínuo $\epsilon \to 0$ , de modo que a lagrangiana terá a forma

$L=\int dx{\frac {1}{2}}\left[\mu {\dot {\phi (t,x)}}^{2}-\nu \left({\frac {d\phi (t,x)}{dx}}\right)^{2}\right]$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

onde $\phi (t,x)$ representa o deslocamento da partícula relativa a posição $�$ no instante de tempo $�$ . Também, define-se as quantidades $\mu =\lim _{\epsilon \to 0}{\frac {m}{\epsilon }}$ $\nu =\lim _{\epsilon \to 0}\kappa \epsilon$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Generalizando essa discussão prévia para um sistema relativístico, tem-se uma lagrangiana que será uma função do campo $\phi (x)$ , em que $x=x^{\mu }$ e das derivadas $\partial _{\mu }\phi (x)$ , dessa maneira, o funcional ação pode ser escrito como

$S=\int dtL(\phi ,\partial _{\mu }\phi )$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Finalmente, a lagrangiana pode ser escrita como

$L(\phi ,\partial _{\mu }\phi )=\int d^{3}x{\mathcal {L}}(\phi ,\partial _{\mu }\phi )$ ,/ $\psi ^{*}$ [ $\psi ^{*}$

onde ${\mathcal {L}}(\phi ,\partial _{\mu }\phi )$ , é conhecida como densidade lagrangiana.^[9] A equação de Euler-Lagrange é:

$\partial _{\mu }{\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\phi )}}-{\frac {\partial {\mathcal {L}}}{\partial \phi }}=0$ ./ $\psi ^{*}$ [ $\psi ^{*}$

Primeiras unificações. Equações relativísticas[editar | editar código-fonte]

Equação de Klein-Gordon[editar | editar código-fonte]

Como foi dito acima, quando Schrödinger primeiro procurou uma equação que regesse os sistemas quânticos, pautou sua busca admitindo uma aproximação relativista, encontrando a depois redescoberta equação de Klein-Gordon:

\left[\square +\left({\frac {mc}{\hbar }}\right)^{2}\right]\psi =0

onde

\square \equiv \eta _{\nu \mu }\partial _{\nu }\partial ^{\nu }

A equação de Klein-Gordon, às vezes chamada de equação de Klein-Fock-Gordon (ou ainda Klein-Gordon-Fock) pode ser deduzida de algumas maneiras diferentes.

Usando-se a definição relativística de energia

E^{2}=\left.p^{2}c^{2}+m^{2}c^{4}\right.

chega-se à equação:

{\sqrt {(-i\mathbf {\nabla } )^{2}+m^{2}}}\psi =i{\frac {\partial }{\partial t}}\psi

Essa expressão, por conter operadores diferenciais sob o radical, além de apresentar dificuldades computacionais, também apresenta dificuldades conceituais, já que se torna uma teoria não-local (pelo fato de a raiz poder ser expressa como uma série infinita). Por ser uma equação de segunda ordem não permite que fique bem definida a questão da normalização da função de onda.

Fock deduziu-a através da generalização da equação de Schrödinger para campos magnéticos (onde as forças dependem da velocidade). Fock e Klein usaram ambos o método de Kaluza-Klein para deduzi-la. O motivo, só mais tarde entendido, da inadequação desta equação ao átomo de hidrogênio é que ela se aplica bem somente a partículas sem carga e de spin nulo.

Equação de Dirac[editar | editar código-fonte]

Em 1928 Paul Dirac obteve uma equação relativística baseada em dois princípios básicos

A equação deveria ser linear na derivada temporal;
A equação deveria ser relativisticamente covariante.

A equação obtida por ele tinha a seguinte forma:

i\hbar {\frac {\partial \psi }{\partial t}}={\frac {\hbar c}{i}}\left(\alpha _{0}mc\psi +\alpha _{1}{\frac {\partial \psi }{\partial x^{1}}}+\alpha _{2}{\frac {\partial \psi }{\partial x^{2}}}+\alpha _{3}{\frac {\partial \psi }{\partial x^{3}}}\right)

\psi ^{*}

onde $\alpha _{0}$ , $\alpha _{1}$ , $\alpha _{2}$ e $\alpha _{3}$ não são números reais ou complexos, mas sim matrizes quadradas com N² componentes. Semelhantemente, as funções $\psi$ são na verdade matrizes coluna da forma

\psi ={\begin{bmatrix}\psi _{1}\\\psi _{2}\\\vdots \\\psi _{N}\end{bmatrix}}

e as matrizes $\alpha _{0}$ , $\alpha _{1}$ , $\alpha _{2}$ e $\alpha _{3}$ devem ser hermitianas.

A equação de Dirac, diferentemente da equação de Klein-Gordon, é uma equação que dá bons resultados para partículas de spin ½. Aliás, um dos sucessos é que esta equação incorpora o spin de forma natural, o que não ocorre com a equação de Schrondinger, onde o spin é admitido posteriormente como uma hipótese ad hoc. Não obstante, isso levou certos autores a afirmarem que o spin é um grau de liberdade relativístico, o que é contestado. Outro sucesso da equação de Dirac foi prever a existência do pósitron, já que a equação previa valores negativos de energia, o que foi inicialmente interpretado, à luz da [[teoria dos buracos], como indicação de elétrons com energias negativas. Essa teoria afirmava que os pósitrons seriam vacâncias produzidas pela promoção desses elétrons para estados com energias positivas. O vácuo é então visto como um mar de elétrons onde eles estariam compactamente colocados. Hoje, entretanto, essa teoria cedeu lugar à questão de criação e aniquilação de partículas num contexto mais geral da quantização canônica dos campos.

Pesquisar este blog

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS [940]

Comportamento da força forte[editar | editar código-fonte]

Lagrangiano[editar | editar código-fonte]

Antes da quebra de simetria eletrofraca[editar | editar código-fonte]

Depois da quebra de simetria eletrofraca[editar | editar código-fonte]

Formulação matemática[editar | editar código-fonte]

Mecânica clássica e mecânica quântica[editar | editar código-fonte]

Teoria Clássica de Campos[editar | editar código-fonte]

Primeiras unificações. Equações relativísticas[editar | editar código-fonte]

Equação de Klein-Gordon[editar | editar código-fonte]

Equação de Dirac[editar | editar código-fonte]

Comentários

Postar um comentário